问题发现

1. 问题发现

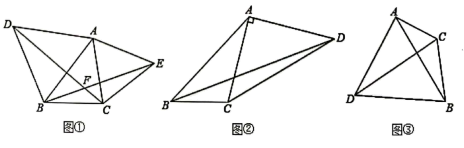
(1) 如图①，已知△ABC，以AB、AC为边向△ABC外分别作等边△ABD和等边△ACE，连接CD，BE．试猜想CD与BE的数量关系是；

(2) 问题探究：如图②，四边形ABCD中，∠ABC＝45°，∠CAD＝90°，AC＝AD，AB＝2BC＝6．求BD的长．

(3) 问题解决：如图③，△ABC中，AC＝2，BC＝3，∠ACB是一个变化的角，以AB为边向△ABC外作等边△ABD，连接CD，求CD的长度最大值．

【考点】

三角形三边关系; 等边三角形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知：线段 $\text{[math]}$ 及过点A的直线l．如果线段 $\text{[math]}$ 与线段 $\text{[math]}$ 关于直线l对称，连接 $\text{[math]}$ 交直线l于点D，以 $\text{[math]}$ 为边作等边 $\text{[math]}$ ，使得点E在 $\text{[math]}$ 的下方，作射线 $\text{[math]}$ 交直线l于点F，连结 $\text{[math]}$ ．

(1) 根据题意补全图形；

(2) 如果 $\text{[math]}$ $\text{[math]}$

① $\text{[math]}$ ▲ ；（用含有 $\text{[math]}$ 代数式表示）

②用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并证明．

综合题普通

2. $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形，当 $\text{[math]}$ 绕点A旋转到图1的位置时，连接连接 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 请猜想线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间有怎样的数量关系？并加以证明；

(2) 将 $\text{[math]}$ 绕点A旋转到图2的位置时，其他条件不变，请直接写出线 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，不需要证明．

综合题普通

3. 如图， $\text{[math]}$ 是等边三角形， $\text{[math]}$ 是等腰三角形，且 $\text{[math]}$ ， $\text{[math]}$ ，以D为顶点作一个60°角，角的两边分别交 $\text{[math]}$ ， $\text{[math]}$ 边于M，N两点，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 至E，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 请在横线上写出角的度数，补充 $\text{[math]}$ 的证明过程．

证明：∵ $\text{[math]}$ 是等边三角形，∴ $\text{[math]}$ $\text{[math]}$ ．

∵ $\text{[math]}$ ， $\text{[math]}$ ， ∴ $\text{[math]}$ $\text{[math]}$ ．

∴ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．

∵ $\text{[math]}$ ， ∴ $\text{[math]}$ $\text{[math]}$ ．

即 $\text{[math]}$ ；

(2) 求证： $\text{[math]}$ ．

综合题普通