在△ABC中，AB＝AC，∠BAC＝90°，点D在射线BC上（不与点B、点C重合），将线段AD绕A逆时针旋转90°得到线段AE，作射线BA与射线CE，两射线交于点F．

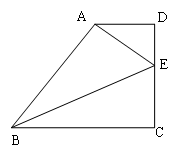
1. 在△ABC中，AB＝AC，∠BAC＝90°，点D在射线BC上（不与点B、点C重合），将线段AD绕A逆时针旋转90°得到线段AE，作射线BA与射线CE，两射线交于点F．

(1) 若点D在线段BC上，如图1，请直接写出CD与EF的关系．

(2) 若点D在线段BC的延长线上，如图2，（1）中的结论还成立吗？请说明理由．

(3) 在（2）的条件下，连接DE，G为DE的中点，连接GF，若tan∠AEC＝ $\text{[math]}$ ， AB＝ $\text{[math]}$ ，求GF的长．

【考点】

三角形全等及其性质; 勾股定理; 锐角三角函数的定义; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图①，有一组平行线l₁∥l₂∥l₃∥l₄ ，正方形ABCD的四个顶点分别在l₁、l₂、l₃、l₄上，EG过点D且垂直于l₁于点E，分别交l₂、l₄于点F、G，EF＝DG＝1，DF＝2.

(1) AE＝，正方形ABCD的边长＝；

(2) 如图②，将∠AED绕点A顺时针旋转α°得到∠AE′D′，且0°＜α＜90°，点D′在直线l₃上，以AD′为边在E′D′左侧作菱形AD′C′B′，使点B′、C′分别在直线l₂、l₄上．

①写出∠B′AD′与α的函数关系并给出证明；

②若α＝30°，求菱形AD′C′B′的边长．

综合题困难

2. 如图，我国某海域上有 $\text{[math]}$ 、 $\text{[math]}$ 两个小岛， $\text{[math]}$ 在 $\text{[math]}$ 的正东方向．有一艘渔船在点 $\text{[math]}$ 处捕鱼，在 $\text{[math]}$ 岛测得渔船在东北方向上，在 $\text{[math]}$ 岛测得渔船在北偏西 $\text{[math]}$ 的方向上，且测得 $\text{[math]}$ 、 $\text{[math]}$ 两处的距离为 $\text{[math]}$ 海里．

(1) 求 $\text{[math]}$ 、 $\text{[math]}$ 两处的距离；

(2) 突然，渔船发生故障，而滞留 $\text{[math]}$ 处等待救援．此时，在 $\text{[math]}$ 处巡逻的救援船立即以每小时 $\text{[math]}$ 海里的速度沿 $\text{[math]}$ 方向前往 $\text{[math]}$ 处，测得 $\text{[math]}$ 在小岛 $\text{[math]}$ 的北偏西 $\text{[math]}$ 方向上距 $\text{[math]}$ 岛 $\text{[math]}$ 海里处．求救援船到达 $\text{[math]}$ 处所用的时间（结果保留根号）．

综合题普通

3. 如图，在梯形 $\text{[math]}$ 中， $\text{[math]}$ ∥ $\text{[math]}$ ， ∠ $\text{[math]}$ =90°， $\text{[math]}$ ， $\text{[math]}$

(1) 求 $\text{[math]}$ 的长；

(2) 若∠ $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点E，连结 $\text{[math]}$ ，求∠ $\text{[math]}$ 的正切值．

综合题普通