1.
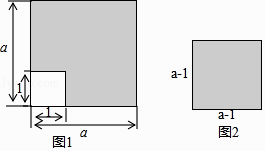
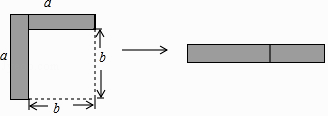
如图所示,回答下列问题.

(1)
大正方形的面积 是多少?
(2)
梯形Ⅱ,Ⅲ的面积
是多少?
(2)
梯形Ⅱ,Ⅲ的面积 ,
,  分别是多少?
(3)
试求
分别是多少?
(3)
试求 与
与 的值;
(4)
由(3)你发现了什么?请用含
的值;
(4)
由(3)你发现了什么?请用含 ,
,  的式子表示你的结论.
的式子表示你的结论.
【考点】
平方差公式的几何背景;
能力提升
真题演练