1.
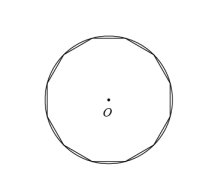
刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若 的半径为1,则这个圆内接正十二边形的面积为( )
的半径为1,则这个圆内接正十二边形的面积为( )

A.
1
B.
3
C.
 D.
D.

【考点】
圆内接正多边形;
基础巩固
能力提升
变式训练
拓展培优
真题演练