1.
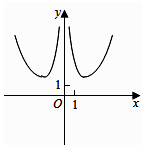
为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改.设企业的污水排放量W与时间t的关系为 , 用
, 用 的大小评价在
的大小评价在 这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.给出下列四个结论,其中正确的结论为( )
这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.给出下列四个结论,其中正确的结论为( )

A.
在 这段时间内,甲企业的污水治理能力比乙企业强
B.
在
这段时间内,甲企业的污水治理能力比乙企业强
B.
在 时刻,甲企业的污水治理能力比乙企业强
C.
在
时刻,甲企业的污水治理能力比乙企业强
C.
在 时刻,甲、乙两企业的污水排放都已达标
D.
甲企业在
时刻,甲、乙两企业的污水排放都已达标
D.
甲企业在 ,
,  ,
,  这三段时间中,在
这三段时间中,在 内的污水治理能力最强
内的污水治理能力最强
【考点】
函数的图象与图象变化;
变式训练
拓展培优
真题演练