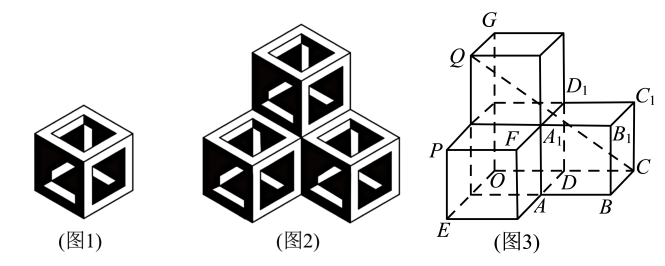
1.
全班学生到工厂劳动实践,各自用  ,
,  的长方体
的长方体  切割出四棱锥
切割出四棱锥  模型.产品标准要求:
模型.产品标准要求:  分别为
分别为  的中点,
的中点,  可以是线段
可以是线段  (不含端点)上的任意一点,有四位同学完成制作后,对自己所做的产品分别作了以下描述,你认为有可能符合标准的是( )
(不含端点)上的任意一点,有四位同学完成制作后,对自己所做的产品分别作了以下描述,你认为有可能符合标准的是( )

A.
使直线  与平面
与平面  所成角取到了最大值
B.
使直线
所成角取到了最大值
B.
使直线  与平面
与平面  所成角取到了最大值
C.
使平面
所成角取到了最大值
C.
使平面  与平面
与平面  的夹角取到了最大值
D.
使平面
的夹角取到了最大值
D.
使平面  与平面
与平面  的夹角取到了最大值
的夹角取到了最大值
【考点】
直线与平面所成的角;
二面角及二面角的平面角;
基础巩固
能力提升
变式训练
拓展培优
真题演练