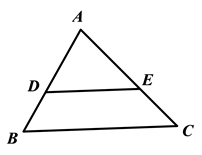1.
如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.

(1)
求证:∠E= ∠C;
(2)
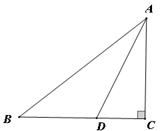
如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)
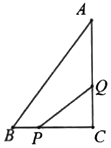
如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数.
∠C;
(2)
如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)
如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数.
【考点】
三角形内角和定理;
三角形的外角性质;
相似三角形的性质;
锐角三角函数的定义;
角平分线的概念;