若四边形的一组对角α，β，满足∠α ∠β＝180°，我们把这个四边形称为可衍生四边形，∠β为二倍角.

1. 若四边形的一组对角α，β，满足∠α $\text{[math]}$ ∠β＝180°，我们把这个四边形称为可衍生四边形，∠β为二倍角.

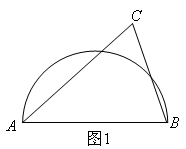
(1) 如图1，在四边形ABCD中，AD⊥CD，∠A＝130°，当四边形ABCD为可衍生四边形，且∠C为二倍角时，求∠B的度数；

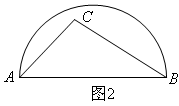
(2) 如图2，四边形ABCD内接于⊙O，点E是圆上一点，连结并延长CE，AD交于点F，延长CD，BA交于点G，CD•DG＝AD•DF，求证：四边形ABCF是可衍生四边形；

(3) 如图3，在（2）的条件下，连结AE，EG，若CD是⊙O的直径，AF⊥EG，AG＝5AB，求sin∠FAG的值.

【考点】

多边形内角与外角; 圆周角定理; 圆内接四边形的性质; 相似三角形的判定与性质; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图， A B 是 $\text{[math]}$ 的直径，弦 CD 交 AB 于点 $\text{[math]}$ ，连接 AC， AD，已知 $\text{[math]}$ .

(1) 求 $\text{[math]}$ 的度数；

(2) 若点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，求 $\text{[math]}$ 的度数.

综合题普通

2. 如图AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺按要求画图．

(1) 在图1中，画出△ABC的三条高的交点；

(2) 在图2中，画出△ABC中AB边上的高．

综合题普通

3. 如图，△ABC内接于 $\text{[math]}$ ，弦CD、BE相交于点 $\text{[math]}$ .

(1) 如图1，求证：AB为 $\text{[math]}$ 的直径；

(2) 如图2，过点 $\text{[math]}$ 作 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(3) 如图3，在(2)的条件下，CD与AB相交于点 $\text{[math]}$ ，连接GH并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接DK，沿DK所在直线作劣弧DK的轴对称图形经过点 $\text{[math]}$ ，求线段DE的长度.

综合题困难