0 返回首页
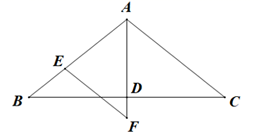
1. 如图，在△ABC中，∠C＝90°，点D是AB边上的一点，DE⊥AB于D，交AC于M，且ED＝AC，过点E作EF∥BC分别交AB、AC于点F、N.

(1) 试说明：△ABC≌△EFD；
(2) 若∠A＝25°，求∠EMN的度数.
【考点】
平行线的性质; 三角形内角和定理; 三角形全等的判定-AAS; 对顶角及其性质; 邻补角;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 如图，在△ABC中，AB＝AC，AD⊥BC于点D．

(1) 若∠C＝40°，求∠BAD的度数；
(2) 若点E在边AB上，EF∥AC交AD的延长线于点F，求证：AE=FE．
综合题 普通
2. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=72°，∠C=30°．

(1) 求∠BAE的度数；
(2) 求∠DAE的度数。
综合题 普通
3. 数学课上老师提出“请对三角形内角和等于180°进行说理.”已知：∠A，∠B，∠C是△ABC的三个内角.对∠A+∠B+∠C=180°进行说理.

(1) 小明给出如下说理过程，请补全证明过程

证明：过点A作AD∥BC

∵AD∥BC

∴∠1=∠C()

同理，=

∵∠1+∠2+∠BAC=180°()

∴∠BAC+∠B+∠C=180°
(2) 听完小明的说理过程后，小亮提出：小明作辅助线的方法，就是借助平行线把三角形的三个内角转化成一个平角，这就启发我们可以借助平行线，对“如图，∠A+∠B+∠C+∠D=360°”进行说理.请你帮助小亮完成作图并写出推理过程.
综合题 普通