已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE＝CF ，点G ， H在对角线BD上，且BG＝DH ．

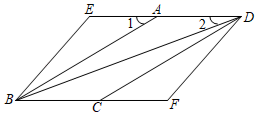
1. 已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE＝CF ，点G ， H在对角线BD上，且BG＝DH ．

(1) 求证：△BFH≌△DEG；

(2) 连接DF ，若DF＝BF ，则四边形EGFH是什么特殊四边形？证明你的结论．

【考点】

菱形的判定; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ .求证：

(1) $\text{[math]}$ ；

(2) 四边形 $\text{[math]}$ 是菱形.

综合题普通

2. 在 $\text{[math]}$ 中， $\text{[math]}$ ， D为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ， $\text{[math]}$ 延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$

(1) 如图1，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(2) 连接 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，依题意补全图2，若 $\text{[math]}$ ，用等式表示线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并证明．

综合题困难

3. 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 相交于点O，点E，F在 $\text{[math]}$ 上，且 $\text{[math]}$ ．连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，判断四边形 $\text{[math]}$ 的形状，并说明理由．

综合题普通