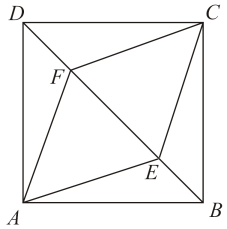
1.
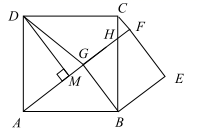
如图,正方形  和正方形
和正方形  有公共顶点
有公共顶点  ,且顶点
,且顶点  ,
,  ,
,  三点共线,顶点
三点共线,顶点  ,
,  ,
,  三点共线,
三点共线,  于点
于点  ,
,  ,
,  .
.
(1)
求证:  ;
(2)
连接
;
(2)
连接  ,求
,求  的长;
(3)
直接写出
的长;
(3)
直接写出  与
与  的面积差.
的面积差.
【考点】
三角形的面积;
勾股定理;
正方形的性质;
能力提升
真题演练


 E
E