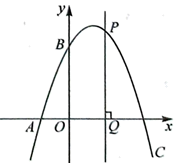
已知在平面直角坐标系xOy中，点A的坐标为（3，4），M是抛物线（）对称轴上的一个动点。小明经探究发现：当的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线（）的对称轴上存在3个不同的点M，使△AOM为直角三角形，则的值是

1. 已知在平面直角坐标系xOy中，点A的坐标为（3，4），M是抛物线 $\text{[math]}$ （ $\text{[math]}$ ）对称轴上的一个动点。小明经探究发现：当 $\text{[math]}$ 的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线 $\text{[math]}$ （ $\text{[math]}$ ）的对称轴上存在3个不同的点M，使△AOM为直角三角形，则 $\text{[math]}$ 的值是

【考点】

二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 在抛物线 $\text{[math]}$ 上，过 $\text{[math]}$ 轴上点 $\text{[math]}$ 作两条相互垂直的直线与抛物线分别交于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 分别是线段 $\text{[math]}$ ， $\text{[math]}$ 的中点， $\text{[math]}$ 面积的最小值为．

填空题困难

2. 平面直角坐标系中，将抛物线 $\text{[math]}$ 平移得到抛物线C，如图所示，且抛物线C经过点 $\text{[math]}$ 和 $\text{[math]}$ ，点P是抛物线C上第一象限内一动点，过点P作x轴的垂线，垂足为Q，则 $\text{[math]}$ 的最大值为．

填空题困难

3. 如图，在Rt△ABC中，∠C=90°，BC=4，BA=5，点D在边AC上的一动点，过点D作DE∥AB交边BC于点E，过点B作BF⊥BC交DE的延长线于点F，分别以DE，EF为对角线画矩形CDGE和矩形HEBF，则在D从A到C的运动过程中，当矩形CDGE和矩形HEBF的面积和最小时，则EF的长度为.

填空题普通