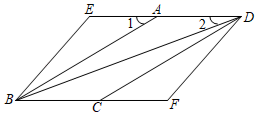
如图，已知菱形ABCD中，分别以C、D为圆心，大于 CD的长为半径作弧，两弧分别相交于M、N两点，直线MN交CD于点F ，交对角线AC于点E ，连接BE、DE ．

1. 如图，已知菱形ABCD中，分别以C、D为圆心，大于 $\text{[math]}$ CD的长为半径作弧，两弧分别相交于M、N两点，直线MN交CD于点F ，交对角线AC于点E ，连接BE、DE ．

(1) 求证：BE＝CE；

(2) 若∠ABC＝72°，求∠ABE的度数．

【考点】

菱形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，四边形ABCD为菱形，E为对角线AC上的一个动点（不与点A，C重合），连接DE并延长交射线AB于点F，连接BE．

(1) 求证： $\text{[math]}$ ；

(2) 求证： $\text{[math]}$ ．

综合题普通

2. 在 $\text{[math]}$ 中， $\text{[math]}$ ， D为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ， $\text{[math]}$ 延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$

(1) 如图1，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(2) 连接 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，依题意补全图2，若 $\text{[math]}$ ，用等式表示线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并证明．

综合题困难

3. 如图，在菱形ABCD中，点E、F分别在BC，CD上，且CE=CF。

(1) 求证：△ABE≌△ADF.

(2) 若∠BAE=∠EAF=40°，求∠AEB的度数。

综合题普通