如图

1. 如图

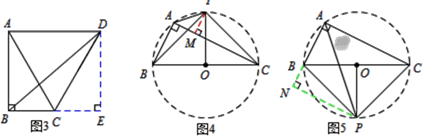
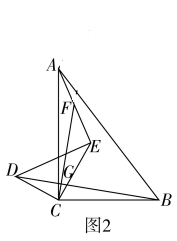
(1) 如图1.在Rt△ACB中，∠ACB＝90°，AC＝8，BC＝6，点D、E分别在边CA，CB上且CD＝3，CE＝4，连接AE，BD，F为AE的中点，连接CF交BD于点G，则线段CG所在直线与线段BD所在直线的位置关系是.（提示：延长CF到点M，使FM＝CF，连接AM）

(2) 将△DCE绕点C逆时针旋转至图2所示位置时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由.

(3) 将△DCE绕点C逆时针在平面内旋转，在旋转过程中，当B，D，E三点在同一条直线上时，CF的长为.

【考点】

旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，等腰Rt△ABC中，BA=BC，∠ABC=90°，点D在AC上，将△ABD绕点B沿顺时针方向旋转90°后，得到△CBE．

(1) 求∠DCE的度数；

(2) 若AB=4，CD=3AD，求DE的长．

综合题普通

问题发现：

(1) 如图1，在Rt△ABC中，∠BAC=30°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC， ∠BCD的度数是；线段BD，AC之间的数量关系是.

(2) 在Rt△ABC中，∠BAC=45°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC，请问（1）中的结论还成立吗？；

(3) 如图3，在Rt△ABC中，AB＝2，AC＝4，∠BDC＝90°，若点P满足PB＝PC，∠BPC＝90°，请直接写出线段AP的长度.

综合题困难

3. 在△ABC中，将边AB绕点A顺时针旋转60°得到线段AD，将边AC绕点A逆时针旋转120°得到线段AE，连接DE.

(1) 、如图①，当∠BAC=90°时，若△ABC的面积为5，则△ADE的面积为；

(2) 如图②，CF、EG分别是△ABC和△ADE的高，若△ABC为任意三角形，△ABC与△ADE的面积是否相等，请说明理由；

(3) 如图④，连接BD、CE.若AB=4，AC=2 $\text{[math]}$ ，四边形CED的面积为13 $\text{[math]}$ ，则△ABC的面积为.

综合题普通