0 返回首页
1.

问题探究：

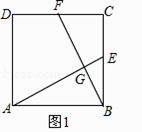
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．

(1) 证明：AD=BE；
(2) 求∠AEB的度数．
(3)

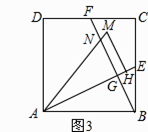
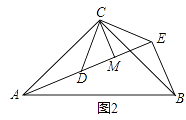
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．（Ⅰ）请求出∠AEB的度数；（Ⅱ）判断线段CM、AE、BE之间的数量关系，并说明理由．
【考点】
三角形全等及其性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1.

已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点O，点P从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：

(1) 当t为何值时，AP=PO．
(2) 设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；
(3) 在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．
综合题 普通
2.

如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．

(1) 求证：AE⊥BF；
(2)

将△BCF沿BF对折，得到△BPF（如图2），延长FP到BA的延长线于点Q，求sin∠BQP的值；
(3)

将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM（如图3），若AM和BF相交于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．
综合题 普通
3.

如图，点B、F、C、E在同一直线上，并且BF=CE，∠B=∠E．

(1) 请你只添加一个条件（不再加辅助线），使得△ABC≌△DEF．
(2) 添加了条件后，证明△ABC≌△DEF．
综合题 普通