1.
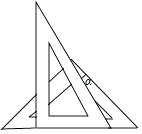
如图所示,在△ABC.D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.

【考点】
三角形内角和定理;
三角形的外角性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练