1.
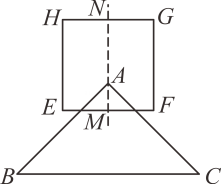
如图,在边长为2的正方形  中,
中,  ,
,  分别为
分别为  与
与  的中点,一个三角形
的中点,一个三角形  沿竖直方向向上平移,在运动的过程中,点
沿竖直方向向上平移,在运动的过程中,点  恒在直线
恒在直线  上,当点
上,当点  运动到线段
运动到线段  的中点时,点
的中点时,点  ,
,  恰与
恰与  ,
,  两边的中点重合.设点
两边的中点重合.设点  到
到  的距离为
的距离为  ,三角形
,三角形  与正方形
与正方形  的公共部分的面积为
的公共部分的面积为  ,则当
,则当  时,
时,  的值为( )
的值为( )
A.
 或
或  B.
B.
 或
或  C.
C.
 D.
D.
 或
或 
【考点】
三角形的面积;
数学思想;
几何图形的面积计算-割补法;







