1.
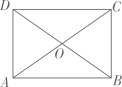
如图①,在▱ABCD中,AD=BD=2,BD⊥AD,点E为对角线AC上一动点,连接DE,将DE绕点D逆时针旋转90°得到DF,连接BF.

(1)
求证:BF=AE;
(2)
若BF所在的直线交AC于点M,求OM的长度;
(3)
如图②,当点F落在△OBC的外部,构成四边形DEMF时,求四边形DEMF的面积.
【考点】
三角形的面积;
矩形的判定与性质;
几何图形的面积计算-割补法;
三角形全等的判定-SAS;
三角形全等的判定-AAS;