如图，点D，E分别在等边△ABC的两边AB，AC上，AD=BE，BD，CE交于点P。CF⊥BD于点F。

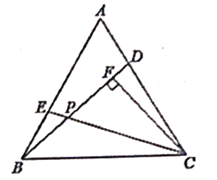
1. 如图，点D，E分别在等边△ABC的两边AB，AC上，AD=BE，BD，CE交于点P。CF⊥BD于点F。

(1) 判断线段BD，CE的数量关系，并证明；

(2) 求∠DPC的度数；

(3) 若CP=10，求PF的长。

【考点】

三角形的外角性质; 全等三角形的判定与性质; 等边三角形的性质; 含30°角的直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，△ABD、△AEC都是等边三角形，直线CD与直线BE交于点F．

(1) 求证：CD=BE；

(2) 求∠CFE的度数．

综合题普通

2. 如图，在△ABC中，∠B=60°，△ABC的角平分线AD、CE相交于点O，

(1) 求∠AOC的度数；

(2) 求证：AE+CD=AC；

(3) 求证：OE=OD．

综合题普通

3. 在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为边向右侧作等边三角形 $\text{[math]}$ ，点 $\text{[math]}$ 的位置随点 $\text{[math]}$ 位置的变化而变化，连接 $\text{[math]}$ ．

(1) 如图①，当点 $\text{[math]}$ 在菱形 $\text{[math]}$ 内部或边上时，求证： $\text{[math]}$ ；

(2) 如图②、图③，请分别写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，不需证明．

综合题普通