1.
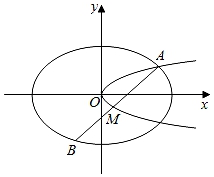
如图,已知椭圆C1:  +y2=1,抛物线C2:y2=2px(p>0),点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C1于点B,交抛物线C2于M(B,M不同于A).
+y2=1,抛物线C2:y2=2px(p>0),点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C1于点B,交抛物线C2于M(B,M不同于A).
(Ⅰ)若p= ,求抛物线C2的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
【考点】
基本不等式在最值问题中的应用;
抛物线的定义;
直线与圆锥曲线的综合问题;
能力提升
变式训练