1.
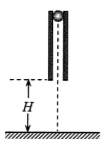
如图,一竖直圆管质量为M,下端距水平地面的高度为H,顶端塞有一质量为m的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知M =4m,球和管之间的滑动摩擦力大小为4mg, g为重力加速度的大小,不计空气阻力。
(1)
求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;
(2)
管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;
(3)
管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。
【考点】
匀变速直线运动的位移与时间的关系;
匀变速直线运动的位移与速度的关系;
牛顿第二定律;
能力提升
真题演练


