1.
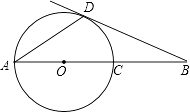
如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.
(1)
直线BD是否与⊙O相切?为什么?
(2)
连接CD,若CD=5,求AB的长.
【考点】
含30°角的直角三角形;
圆周角定理;
切线的判定;