1.
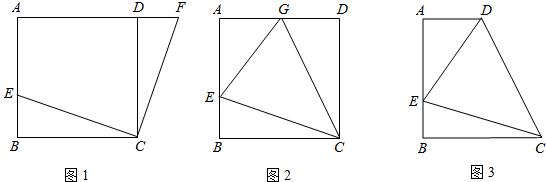
如图,现有一张边长为8的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连结BP、BH.

(1)
求证:∠APB=∠BPH;
(2)
求证:AP+HC=PH;
(3)
当AP=2时,求PH的长.
【考点】
全等三角形的判定与性质;
勾股定理;
正方形的性质;
翻折变换(折叠问题);