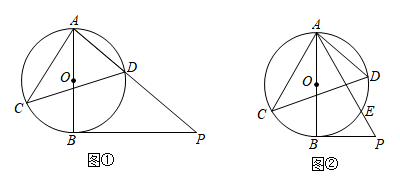如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．

1. 如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．

(1) 求证：KE=GE；

(2) 若KG²=KD•GE，试判断AC与EF的位置关系，并说明理由；

(3) 在（2）的条件下，若sinE= $\text{[math]}$ ，AK=2 $\text{[math]}$ ，求FG的长．

【考点】

勾股定理; 圆周角定理; 切线的性质; 相似三角形的判定与性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 都是 $\text{[math]}$ 的半径， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的半径．

综合题普通

2. 如图， $\text{[math]}$ 半径为2，弦 $\text{[math]}$ ， A是弦 $\text{[math]}$ 所对优弧上的一个点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 点M，连接 $\text{[math]}$ ，过点B作 $\text{[math]}$ ，垂足为E．

(1) 求证： $\text{[math]}$ ．

(2) 过点A作 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点H，D．求 $\text{[math]}$ 的长．

综合题普通

3. 如图，AB为⊙O直径，△ACD是⊙O的内接三角形，PB切⊙O于点B．

(1) 如图①，延长AD交PB于点P，若∠C=40°，求∠P和∠BAP的度数；

(2) 如图②，连接AP交⊙O于点E，若∠D=∠P，弧CE=弧AC，求∠P和∠BAP的度数．

综合题普通