0 返回首页
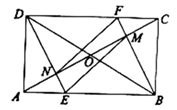
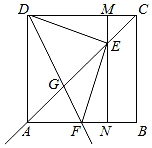
1. 矩形ABCD中，DE平分∠ADC交BC边于点E，P为DE上的一点（PE＜PD），PM⊥PD，PM交AD边于点M．

(1) 若点F是边CD上一点，满足PF⊥PN，且点N位于AD边上，如图1所示．

求证：①PN=PF；②DF+DN= DP；
(2) 如图2所示，当点F在CD边的延长线上时，仍然满足PF⊥PN，此时点N位于DA边的延长线上，如图2所示；试问DF，DN，DP有怎样的数量关系，并加以证明．
【考点】
全等三角形的判定与性质; 矩形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图，矩形ABCD ， 过点B作BE∥AC交DC的延长线于点E ． 过点D作DH⊥BE于H ， G为AC中点，连接GH ．

(1) 求证：BE＝AC ．
(2) 判断GH与BE的数量关系并证明．
综合题 普通
2. 如图，已知四边形ABCD是矩形，延长AB至点F，连结CF，使得CF=AF，过点A作AE⊥FC于点E.

(1) 求证：AD=AE.
(2) 连结CA，若∠DCA=70°，求∠CAE的度数.
综合题 普通
3. 如图，在矩形ABCD中，E是BC上一点，且AE＝BC，DF⊥AE，垂足是F，连接DE.

求证：

(1) DF＝AB；
(2) DE是∠FDC的平分线.
综合题 普通