1.
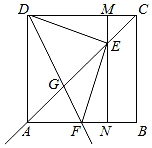
如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)
求证:EF=DE;
(2)
当AF=2时,求GE的长.
【考点】
全等三角形的判定与性质;
矩形的性质;
正方形的性质;
相似三角形的判定与性质;