1.
定义:我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”.
性质:“朋友三角形”的面积相等.
如图1,在△ABC中,CD是AB边上的中线.
那么△ACD和△BCD是“朋友三角形”,并且S△ACD=S△BCD .
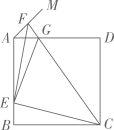
应用:如图2,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=AD=4,BC=6,点E在BC上,点F在AD上,BE=AF,AE与BF交于点O.

(1)
求证:△AOB和△AOF是“朋友三角形”;
(2)
连接OD,若△AOF和△DOF是“朋友三角形”,求四边形CDOE的面积.
拓展:如图3,在△ABC中,∠A=30°,AB=8,点D在线段AB上,连接CD,△ACD和△BCD是“朋友三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的 ,则△ABC的面积是(请直接写出答案).
【考点】
三角形全等的判定;