0 返回首页
1. 将一张矩形纸条ABCD按如图所示折叠，若折叠角∠FEC=64°．

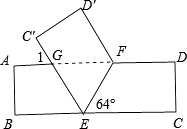
(1) 求∠1的度数；
(2) 求证：△EFG是等腰三角形．
【考点】
翻折变换（折叠问题）;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角.

(1) 如图2，在△ABC中，∠B>∠C，若经过两次折叠，∠BAC是△ABC的好角，则∠B与∠C的等量关系是；
(2) 如果一个三角形的最小角是20°，则此三角形的最大角为时，该三角形的三个角均是此三角形的好角。
综合题 困难
2. ABCD是长方形纸片的四个顶点，点E、F、H分别是边AB、BC、AD上的三点，连结EF、FH．

(1) 将长方形纸片的ABCD按如图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′，点B′在F C′上，则∠EFH的度数为；
(2) 将长方形纸片的ABCD按如图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′（B′、C′的位置如图所示），若∠B′FC′=18°，求∠EFH的度数；
(3) 将长方形纸片的ABCD按如图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′（B′、C′的位置如图所示），若∠EFH=β°，求∠B′FC′的度数为．
综合题 普通
3. 如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．


(1) 试判断△BDE的形状，并说明理由；
(2) 若AB=3，AD=9，求△BDE的面积           
综合题 普通