在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图．

1.

在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图．

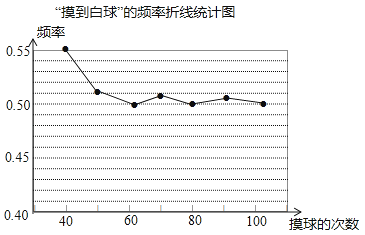
(1) 请估计：当n很大时，摸到白球的概率将会接近　（精确到0.01），假如你摸一次，你摸到白球的概率为

(2) 试估算盒子里白、黑两种颜色的球各有多少个？

(3) 在（2）条件下如果要使摸到白球的概率为 $\text{[math]}$ ，需要往盒子里再放入多少个白球？

【考点】

利用频率估计概率;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明设计了一个如下方法：

①在此封闭图形内画出一个半径为1米的圆．

②在此封闭图形旁边闭上眼睛向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：

掷小石子落在不规则图形内的总次数	50	150	300	500	…
小石子落在圆内（含圆上）的次数m	20	59	123	203	…
小石子落在圆外的阴影部分（含外缘）的次数n	29	91	176	293	…
m：n	0.689	0.694	0.689	0.706

(1) 通过以上信息，可以发现当投掷的次数很大时，则m：n的值越来越接近（结果精确到0.1）．

(2) 若以小石子所落的有效区域为总数（即m+n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在附近（结果精确到0.1）．

(3) 请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是多少平方米？（结果保留π）

综合题普通

2. 在同样的条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表.

实验种子数（粒）	1	5	50	100	200	500	1000	2000	3000
发芽频数	0	4	45	92	188	476	951	1900	2850

(1) 估计该麦种的发芽概率.

(2) 如果播种该种小麦每公顷所需麦苗数为4000000棵，种子发芽后的成秧率为80%，该麦种的千粒质量为50g.那么播种3公顷该种小麦，估计约需麦种多少千克（精确到1kg）？

综合题普通

3. 在一个不透明的盒子里装着只有颜色不同的黑、白两种球共5个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一球记下颜色，再把它放回盒子，不断重复上述过程实验n次，下表是小明“摸到白球”的频数、频率统计表.

摸球实验次数n	10	100	150	200	500	…
摸到白球的频数m	2	22	31	39	101	…
摸到白球的频率p	0.200	0.220	0.207	0.195	0.202	…

(1) 观察上表，可以推测，摸一次摸到白球的概率为.

(2) 请你估计盒子里白球个数.

(3) 若往盒子中同时放入x个白球和y个黑球，从盒子中随机取出一个白球的概率是0.25，求y与x之间的函数关系式.

综合题普通