1.
已知△ABC是等边三角形.
(1)
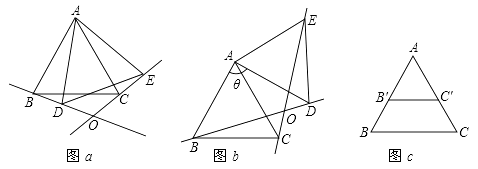
将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(2)
如图c,在AB和AC上分别截取点B′和C′,使AB=  AB′,AC=
AB′,AC=  AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
①如图a,当θ=20°时,△ABD与△ACE是否全等?(填“是”或“否”),∠BOE=度;
【考点】
全等三角形的判定与性质;
等边三角形的性质;
旋转的性质;