1.
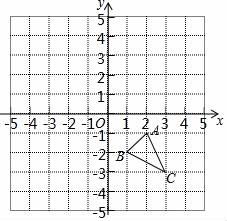
在平面直角坐标系中,△ABC的顶点坐标A(﹣4,1),B(﹣2,1),C(﹣2,3)
(1)作△ABC关于y轴的对称图形△A1B1C1;
(2)将△ABC向下平移4个单位长度,作出平移后的△A2B2C2;
(3)求四边形AA2B2C的面积.

【考点】
作图﹣轴对称;
作图﹣平移;
基础巩固
能力提升
变式训练
拓展培优
真题演练