1.
已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1 , h2 , h3 , △ABC的高为h.

(1)
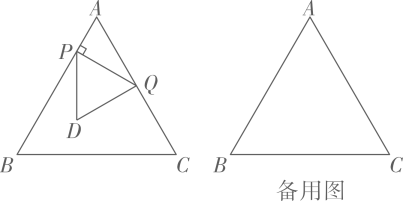
若点P在一边BC上,如图①,此时h3=0,求证:h1+h2+h3=h;
(2)
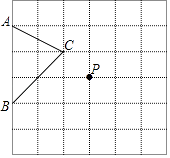
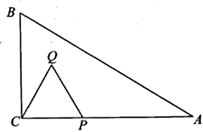
当点P在△ABC内,如图②,以及点P在△ABC外,如图③,这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1 , h2 , h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
【考点】
三角形的面积;
等边三角形的性质;