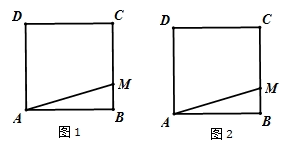
1.
如图所示,在平面直角坐标系中,正方形  的点
的点  、
、  分别在
分别在  轴和
轴和  轴的正半轴上,点
轴的正半轴上,点  在第一象限,
在第一象限,  平分
平分  交
交  于
于  .
.

(1)
求  的度数和
的度数和  的长;
(2)
点
的长;
(2)
点  不动,将正方形
不动,将正方形  绕点
绕点  逆时针旋转至图
逆时针旋转至图  的位置,
的位置,  ,
,  交
交  于点
于点  ,连接
,连接  .求证:
.求证:  ;
(3)
如图
;
(3)
如图  ,在(2)的条件下,正方形的边
,在(2)的条件下,正方形的边  交
交  轴于点
轴于点  、
、  平分
平分  ,
,  、
、  是
是  、
、  上的动点,求
上的动点,求  的最小值,请在图中画出示意图并简述理由.
的最小值,请在图中画出示意图并简述理由.
【考点】
全等三角形的判定与性质;
等边三角形的判定;
正方形的性质;
轴对称的应用-最短距离问题;
旋转的性质;