0 返回首页
1. 在△ABC中，D、E分别是AB，AC的中点，作∠B的角平分线

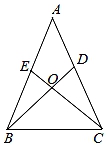
(1) 如图1，若∠B的平分线恰好经过点E，猜想△ABC是怎样的特殊三角形，并说明理由；
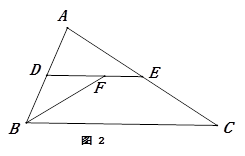
(2) 如图2，若∠B的平分线交线段DE于点F，已知AB=8，BC=10，求EF的长度；
(3) 若∠B的平分线交直线DE于点F，直接写出AB、BC、EF三者之间的数量关系。
【考点】
全等三角形的判定与性质; 等腰三角形的判定;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 图1和图2中的正方形ABCD和四边形AEFG都是正方形。

(1) 如图1，连接DE，BG，M为线段BG的中点，连接AM，探究AM与DE的数量关系和位置关系，并证明你的结论；
(2) 在图1的基础上，将正方形AEFG绕点A逆时针方向旋转到图2的位置，连结DE、BG，M为线段BG的中点，连结AM，探究AM与DE的数量关系和位置关系，并证明你的结论。
综合题 普通
2. 如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN ， 连接EN、AM、CM ，

(1) 求证：△AMB≌△ENB；
(2) 当M点在何处时，AM +CM的值最小，并说明理由；
(3) 当M点在何处时，AM +BM +CM的值最小，并说明理由；
综合题 普通
3. 如图，△ABC中，D是AB上一点，DE⊥AC于点E ， F是AD的中点，FG⊥BC于点G ， 与DE交于点H ， 若FG＝AF ， AG平分∠CAB ， 连接GE ， GD ．

(1) 求证：△ECG≌△GHD；
(2) 小亮同学经过探究发现：AD＝AC+EC ． 请你帮助小亮同学证明这一结论．
(3) 若∠B＝30°，判定四边形AEGF是否为菱形，并说明理由．
综合题 困难