1.
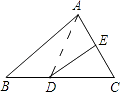
如图①,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°
, 则有结论EF=BE+FD成立;
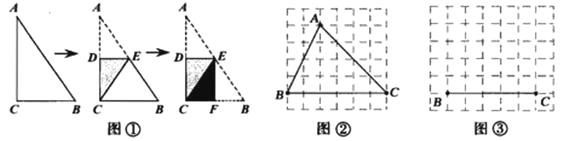
(1)如图②,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC、CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;若不成立,请说明理由;
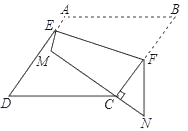
(2)若将(1)中的条件改为:在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.



【考点】
翻折变换(折叠问题);