1.
问题情境:小明和小丽共同探究一道数学题:如图①,在△ABC中,点D是边BC的中点,∠BAD = 65°,∠DAC = 50°,AD = 2,求AC的长为多少.

(1)
探索发现;
(2)
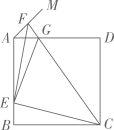
类比应用:如图②,

在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,AB⊥AC.若∠CAD=45°,∠ADC = 67.5°,AO = 2,则BC的长为.
小明的思路是:延长AD至点E , 使DE = AD , 构造全等三角形.
小丽的思路是:过点C作CE∥AB , 交AD的延长线于点E , 构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.

在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,AB⊥AC.若∠CAD=45°,∠ADC = 67.5°,AO = 2,则BC的长为.
【考点】
三角形全等的判定;
能力提升
真题演练