0 返回首页
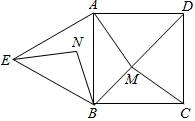
1. 如图，在正方形ABCD中，E为对角线BD上的一点，点F在AD的延长线上，且∠CEF=90°，EF交CD于H，分别过点F，点C作EC和EF的平行线，交于点G.

(1) 证明：AE=CE；
(2) 证明：四边形ECGF是正方形；
(3) 若正方形ABCD的边长为 ，且BE=BC，求此时ΔEDF的面积.
【考点】
全等三角形的判定与性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 图1和图2中的正方形ABCD和四边形AEFG都是正方形。

(1) 如图1，连接DE，BG，M为线段BG的中点，连接AM，探究AM与DE的数量关系和位置关系，并证明你的结论；
(2) 在图1的基础上，将正方形AEFG绕点A逆时针方向旋转到图2的位置，连结DE、BG，M为线段BG的中点，连结AM，探究AM与DE的数量关系和位置关系，并证明你的结论。
综合题 普通
2. 如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN ， 连接EN、AM、CM ，

(1) 求证：△AMB≌△ENB；
(2) 当M点在何处时，AM +CM的值最小，并说明理由；
(3) 当M点在何处时，AM +BM +CM的值最小，并说明理由；
综合题 普通
3. 如图，△ABC中，D是AB上一点，DE⊥AC于点E ， F是AD的中点，FG⊥BC于点G ， 与DE交于点H ， 若FG＝AF ， AG平分∠CAB ， 连接GE ， GD ．

(1) 求证：△ECG≌△GHD；
(2) 小亮同学经过探究发现：AD＝AC+EC ． 请你帮助小亮同学证明这一结论．
(3) 若∠B＝30°，判定四边形AEGF是否为菱形，并说明理由．
综合题 困难