1.
已知:在△ABC外分别以AB,AC为边作△AEB与△AFC.
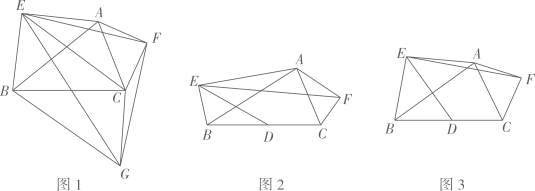
(1)
如图1,△AEB与△AFC分别是以AB,AC为斜边的等腰直角三角形,连接EF.以EF为直角边构造Rt△EFG,且EF=FG,连接BG,CG,EC.
(2)
小明受到图1的启发做了进一步探究:
(3)
小颖受到启发也做了探究:
求证:①△AEF≌△CGF;②四边形BGCE是平行四边形.
如图2,在△ABC外分别以AB,AC为斜边作Rt△AEB与Rt△AFC,并使∠FAC=∠EAB=30°,取BC的中点D,连接DE,EF后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出 的值及∠DEF的度数.
如图3,在△ABC外分别以AB,AC为底边作等腰三角形AEB和等腰三角形AFC,并使∠CAF+∠EAB=90°,取BC的中点D,连接DE,EF后发现,当给定∠EAB=α时,两者间也存在一定的数量关系且夹角度数一定,若AE=m,AB=n,请你帮助小颖用含m,n的代数式直接写出 的值,并用含α的代数式直接表示∠DEF的度数.
【考点】
全等三角形的判定与性质;
平行四边形的判定与性质;
相似三角形的判定与性质;
同角三角函数的关系;
等腰直角三角形;


