如图，已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝1，BC＝2，CD＝1＋，过A作AE⊥CD，垂足为E，现将△ADE沿AE折叠，使得DE⊥EC.

1. 如图，已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝1，BC＝2，CD＝1＋ $\text{[math]}$ ，过A作AE⊥CD，垂足为E，现将△ADE沿AE折叠，使得DE⊥EC.

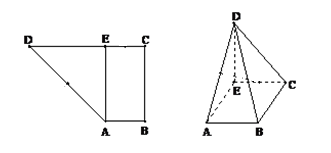
(1) 求证：BC⊥面CDE；

(2) 在线段AE上是否存在一点R，使得面BDR⊥面DCB，若存在，求出点R的位置；若不存在，请说明理由.

【考点】

直线与平面垂直的判定; 平面与平面垂直的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图，在四棱锥 $\text{[math]}$ 中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ．四边形 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ 为侧棱 $\text{[math]}$ 的中点， $\text{[math]}$ 为侧棱 $\text{[math]}$ 上的任意一点．

(1) 若 $\text{[math]}$ 为 $\text{[math]}$ 的中点，求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 是否存在点 $\text{[math]}$ ，使得直线 $\text{[math]}$ 与平面 $\text{[math]}$ 垂直？若存在，写出证明过程并求出线段 $\text{[math]}$ 的长；若不存在，请说明理由．

解答题普通

2. 如图， $\text{[math]}$ 是圆 $\text{[math]}$ 的直径，点 $\text{[math]}$ 是圆 $\text{[math]}$ 上异于 $\text{[math]}$ ， $\text{[math]}$ 的点，直线 $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是线段 $\text{[math]}$ ， $\text{[math]}$ 的中点．

(1) 证明：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 记平面 $\text{[math]}$ 与平面 $\text{[math]}$ 的交线为 $\text{[math]}$ ，试判断直线 $\text{[math]}$ 与直线 $\text{[math]}$ 的位置关系，并说明理由．

解答题普通

3. 如图在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 面ABCD，底面ABCD为菱形，且∠ABC=60°，E为CD的中点，F为PD上一点.

(1) 求证：BD⊥平面PAC；

(2) 求证：平面PAB⊥平面FAE；

解答题普通