0 返回首页
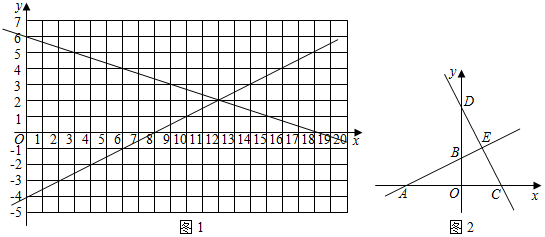
1. 如图，在平面直角坐标系中，直线 分别交x轴、y轴于点B，C，正方形AOCD的顶点D在第二象限内，E是BC中点，OF⊥DE于点F，连结OE．动点P在AO上从点A向终点O匀速运动，同时，动点Q在直线BC上从某点Q1向终点Q2匀速运动，它们同时到达终点．

(1) 求点B的坐标和OE的长；
(2) 设点Q2为(m ， n)，当 tan∠EOF时，求点Q2的坐标；
(3) 根据（2）的条件，当点P运动到AO中点时，点Q恰好与点C重合．①延长AD交直线BC于点Q3 ， 当点Q在线段Q2Q3上时，设Q3Q＝s ， AP＝t ， 求s关于t的函数表达式．②当PQ与△OEF的一边平行时，求所有满足条件的AP的长．
【考点】
一次函数图象与几何变换; 勾股定理; 相似三角形的性质; 一次函数图象与坐标轴交点问题; 一次函数中的动态几何问题;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，Q为AB的中点．动点P从点A出发沿折线AC--CB以每秒2个单位长度的速度运动，连结PQ，以PQ为边构造正方形PMNQ且边MN与点B始终在边PQ同侧．设点P的运动时间为t秒(>0)．

(1) 线段AB的长为
(2) 当点P在边AC上运动时，线段CP的长为      ▲ (用含t的代数式表示) ．

①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．

②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．
(3) 当点P不与点C重合时，作点C关于直线PQ的对称点C'当PC'⊥AB时，直接写出t的值．
综合题 普通
2. 在三角形中，一个角两夹边的平方和减去它对边的平方所得的差，叫做这个角的勾股差.

(1) 概念理解：在直角三角形中，直角的勾股差为；在底边长为2的等腰三角形中，底角的勾股差为；
(2) 性质探究：如图1， 是 的中线， ，记 中 的勾股差为 中 的勾股差为 ；

①求 的值（用含 的代数式表示）；

②试说明 与 互为相反数；
(3) 性质应用：如图2，在四边形 中，点 与 分别是 与 的中点，连接 ，若 ，且 ，求 的值.
综合题 普通
3. 一般地，对于已知一次函数y1=ax+b，y2=cx+d（其中a，b，c，d为常数，且ac＜0），定义一个新函数y= ，称y是y1与y2的算术中项，y是x的算术中项函数.

(1) 如：一次函数y1= x﹣4，y2=﹣ x+6，y是x的算术中项函数，即y= .

①自变量x的取值范围是，当x=时，y有最大值；

②根据函数研究的途径与方法，请填写下表，并在图1中描点、连线，画出此函数的大致图象；

x

8

9

10

12

13

14

16

17

18

y

0

1.2

1.6

2.04

2

1.2

0

③请写出一条此函数可能有的性质；
(2) 如图2，已知一次函数y1= x+2，y2=﹣2x+6的图象交于点E，两个函数分别与x轴交于点A，C，与y轴交于点B，D，y是x的算术中项函数，即y= .

①判断：点A、C、E是否在此算术中项函数的图象上；

②在平面直角坐标系中是否存在一点，到此算术中项函数图象上所有点的距离相等，如果存在，请求出这个点；如果不存在，请说明理由.
综合题 困难