1.
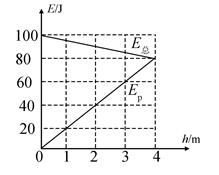
从地面竖直向上抛出一物体,其机械能E总等于动能Ek与重力势能Ep之和。取地面为重力势能零点,该物体的E总和Ep随它离开地面的高度h的变化如图所示。重力加速度取10 m/s2。由图中数据可得( )
A.
物体的质量为2 kg
B.
h=0时,物体的速率为20 m/s
C.
h=2 m时,物体的动能Ek=40 J
D.
从地面至h=4 m,物体的动能减少100 J
【考点】
动能和势能的相互转化;
机械能守恒定律;
能力提升
变式训练
拓展培优