已知点A（0，4）、C（﹣2，0）在直线l：y＝kx+b上，l和函数y＝﹣4x+a的图象交于点B。

0 返回首页

1. 已知点A（0，4）、C（﹣2，0）在直线l：y＝kx+b上，l和函数y＝﹣4x+a的图象交于点B。

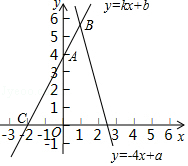
(1) 求直线l的表达式；

(2) 若点B的横坐标是1，求关于x、y的方程组 $\text{[math]}$ 的解及a的值．

(3) 若点A关于x轴的对称点为P，求△PBC的面积．

【考点】

一次函数图象与几何变换; 待定系数法求一次函数解析式; 一次函数与二元一次方程（组）的关系;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 综合应用

如图，直线 $\text{[math]}$ ： $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．直线 $\text{[math]}$ 过点 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．

(1) 求直线 $\text{[math]}$ 的表达式；

(2) 求出 $\text{[math]}$ 轴上的点 $\text{[math]}$ 的坐标，使得 $\text{[math]}$ ；

(3) 求出第一象限内的点 $\text{[math]}$ ，使得 $\text{[math]}$ ．

综合题困难

2. 如图， $\text{[math]}$ ， $\text{[math]}$ 分别表示两个一次函数的图象，它们相交于点P．

(1) 求出两条直线的函数关系式

(2) 点P的坐标可看作是哪个二元一次方程组的解．

综合题普通

3. 已知y与x之间成正比例关系，且当x＝-1时，y＝3．

(1) 求y与x之间的函数关系式；

(2) 当x＝2时，求y的值．

综合题普通