1.
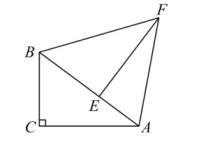
如图,E为正方形ABCD内一点,∠AEB=135°,△AEB按顺时针方向旋转一个角度后成为△CFB,图中是旋转中心,若BE=1,则EF=.

【考点】
勾股定理;
图形的旋转;
基础巩固
能力提升
变式训练
拓展培优