1.
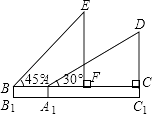
如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)
当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)
当她从点A跑动9  米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10  米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
【考点】
解直角三角形的实际应用﹣仰角俯角问题;
能力提升
真题演练