1.
定义提出：有一组邻边相等的凸四边形叫做“等邻边四边形”
(1)
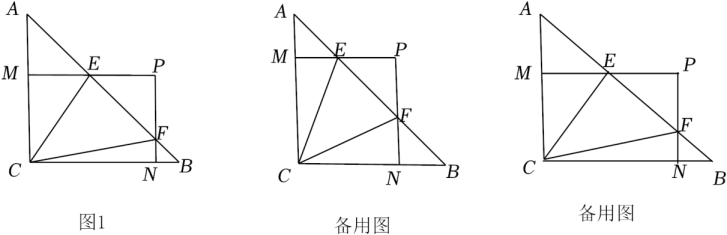
如图1，在3x3的正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，线段AB、BC的端点均在格点上，在图1的方格纸中画出一个等邻边四边形ABCD，要求：点D在格点上；
(2)
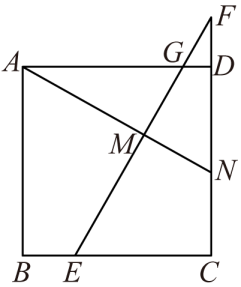
如图2，在等邻边四边形ABCD中，
， 求CD的长；
(3)
如图3，在平面直角坐标系中，矩形OABC的顶点A、C分别在x、y轴正半轴上，已知OC=4，0A=6，D是OA的中点，在矩形OABC内或边上，是否存在点，使四边形OCED为面积最大的“等邻边四边形”，若存在，请求出四边形OCED的最大面积及此时点E的坐标；若不存在，请说明理由.
【考点】
勾股定理;
四边形的综合;
能力提升
真题演练
