1.
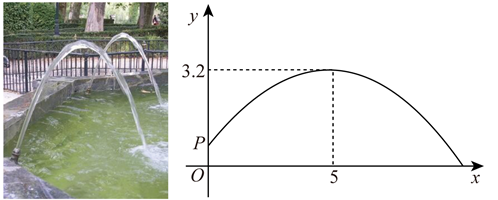
某游乐园要建造一个直径为26m的圆形喷水池,计划在喷水池的周边安装一圈喷水头,使喷出的水柱距池中心5m处达到最高,高度为8m.

(1)
以水平方向为x轴,喷水池中心为原点建立直角坐标系,求在y轴右侧抛物线的函数表达式;
(2)
要在喷水池的中心设计一个装饰物,使各方向喷出的水柱在此汇合,求这个装饰物的设计高度.
【考点】
二次函数的实际应用-喷水问题;
能力提升
真题演练