1.
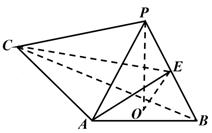
已知四棱锥 分别为
分别为 的中点,
的中点, 平面
平面 .
.

(1)
若 , 证明:
, 证明: 平面
平面 ;
(2)
若
;
(2)
若 , 二面角
, 二面角 的大小为
的大小为 , 求
, 求 .
.
【考点】
直线与平面平行的判定;
用空间向量研究二面角;