1.
探究归纳题:

(1)
如图1,经过四边形的一个顶点可以作 条对角线,它把四边形分成 个三角形;
(2)
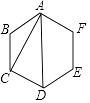
如图2,经过五边形的一个顶点可以作 条对角线,它把五边形分成 个三角形;
(3)
探索归纳:对于 边形
边形 , 过一个顶点可以作 条对角线,它把
, 过一个顶点可以作 条对角线,它把 边形分成 个三角形;(用含
边形分成 个三角形;(用含 的式子表示)
(4)
如果经过多边形的一个顶点可以作100条对角线,那么这个多边形的边数为 .
的式子表示)
(4)
如果经过多边形的一个顶点可以作100条对角线,那么这个多边形的边数为 .
【考点】
多边形的对角线;
 (注:此为
(注:此为