1.
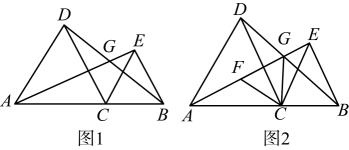
如图 ,
,  是边长为
是边长为 厘米的等边三角形,点
厘米的等边三角形,点 ,
,  分别从顶点
分别从顶点 ,
,  同时出发,沿线段
同时出发,沿线段 ,
,  运动,且它们的速度都为
运动,且它们的速度都为 厘米
厘米 秒.当点
秒.当点 到达点
到达点 时,
时, 、
、 两点停止运动.设点
两点停止运动.设点 的运动时间为
的运动时间为 .
.

(1)
当运动时间为 秒时,
秒时, 的长为________厘米,
的长为________厘米, 的长为________厘米;
的长为________厘米; 用含
用含 的式子表示
的式子表示 (2)
当
(2)
当 为何值时,
为何值时, 是直角三角形;
(3)
如图
是直角三角形;
(3)
如图 , 连接
, 连接 、
、 , 相交于点
, 相交于点 , 则点
, 则点 ,
,  在运动的过程中,
在运动的过程中, 会变化吗?若变化,则说明理由;若不变,请求出它的度数.
会变化吗?若变化,则说明理由;若不变,请求出它的度数.
【考点】
等边三角形的性质;
含30°角的直角三角形;
三角形全等的判定-SAS;