1.
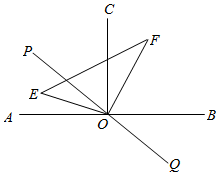
如图,直线AB⊥OC于点O , ∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP , 现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E'OF' , 同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P'Q' , 设运动时间为m秒(0≤m≤20),当直线P'Q'平分∠E'OF'时,则∠COP'=.
【考点】
一元一次方程的其他应用;
角的运算;
旋转的性质;
角平分线的概念;
基础巩固
能力提升
变式训练
拓展培优




